Student Performance Analysis

import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
plt.style.use('ggplot')

The fictional data about student performance can be found on Kaggle (https://www.kaggle.com/spscientist/students-performance-in-exams)

df = pd.read_csv("StudentsPerformance.csv") # Loading the data

1. First look at the data

To get a concise summary of the dataframe

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 8 columns):
 #   Column                       Non-Null Count  Dtype 
---  ------                       --------------  ----- 
 0   gender                       1000 non-null   object
 1   race/ethnicity               1000 non-null   object
 2   parental level of education  1000 non-null   object
 3   lunch                        1000 non-null   object
 4   test preparation course      1000 non-null   object
 5   math score                   1000 non-null   int64 
 6   reading score                1000 non-null   int64 
 7   writing score                1000 non-null   int64 
dtypes: int64(3), object(5)
memory usage: 62.6+ KB

The summary includes list of all columns with their data types and the number of non-null values in each column.

Categorical variables: gender, race/ethnicity, parental level of education, lunch, and test preparation course

Numerical variables: math score, reading score, and writing score

df.shape

(1000, 8)

For quickly testing if your object has the right type of data in it

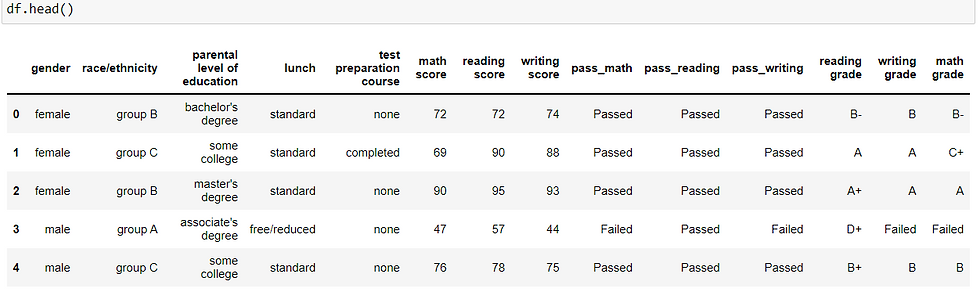
df.head()

Column Name Description

gender: Male/ Female

race/ethnicity: Group division from A to E

parental level of education: Details of parental education varying from high school to master's degree

lunch: Type of lunch selected

test preparation course: Course details

math score: Marks secured by a student in Mathematics

reading score: Marks secured by a student in Reading

writing score: Marks secured by a student in Writing

Examine missing values

df.isna().sum()

There is no missing value in the dataset.

2. Initial data exploration

In this case, the aim is not to create stunning charts.

The charts are used to give a picture of data.

The initial data exploration are essentially univariate, bivariate, and multivariates analysis.

2.1. Univariate analysis

For univariate, we will examine each and every single variable using appropriate chart for each type of variable.

2.1.1. Categorical variables

How many categories for each categorical column ?

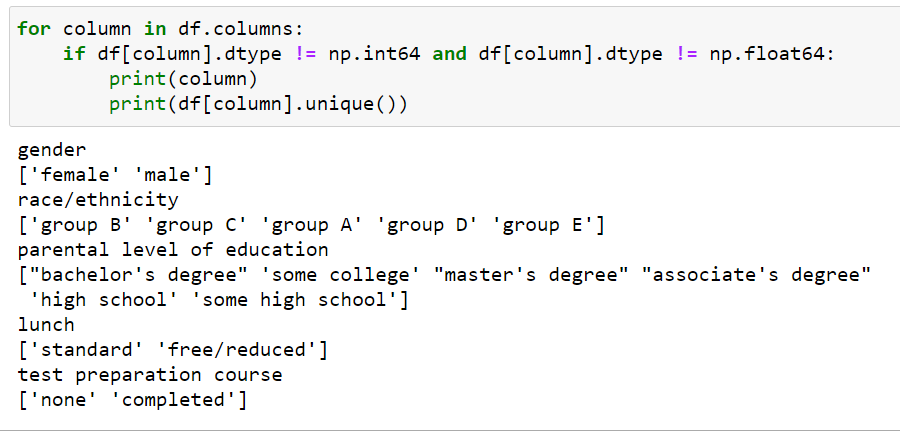
There are five categorical variables in the data set:

gender : 'female', 'male'
race/ethnicity: 'group B', 'group C', 'group A', 'group D', 'group E'
parental level of education: 'bachelor's degree', 'some college', 'master's degree', 'associate's degree', 'high school', 'some high school'
lunch: 'standard', 'free/reduced'
test preparation course: 'none', 'completed'

Visualization of distribution of categorical variables

As there are maximum of 5 categories for a few variables (race/ethnicity and parental level of education). We can use pie chart to see the proportion of these categories.

Visualization of numerical variables

math score
reading score
writing score

Calculating mean across groups

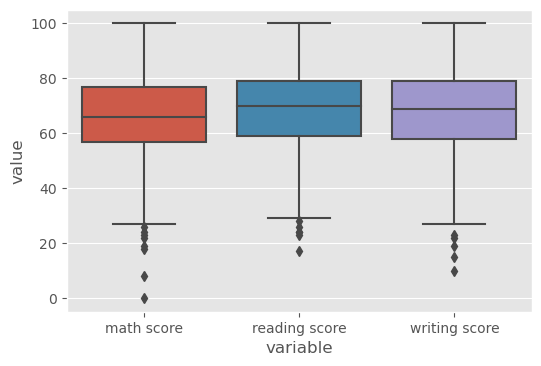
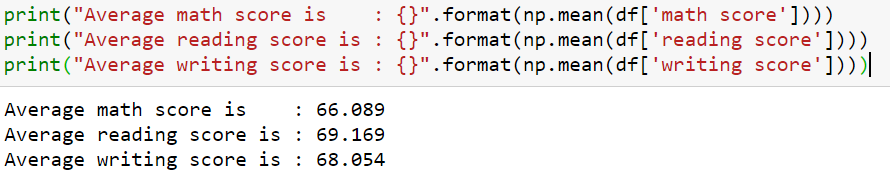
There are three tests: math, reading, and writing. The mean score for the three test are 66, 69, and 68, respectively.

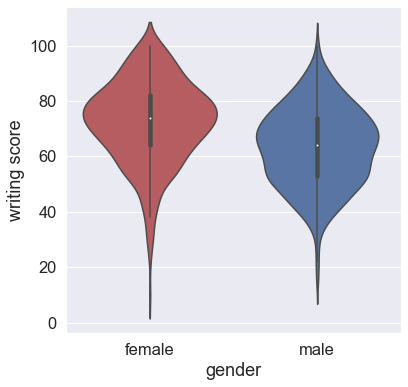
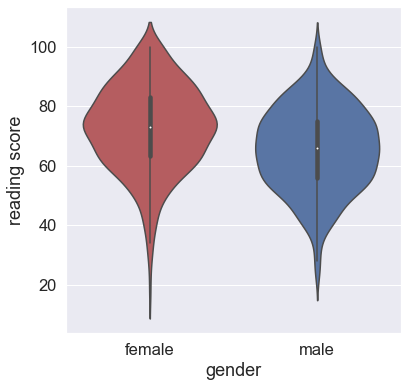
We can also use violin chart to visualize the probability density of the data at different values, usually smoothed by a kernel density estimator

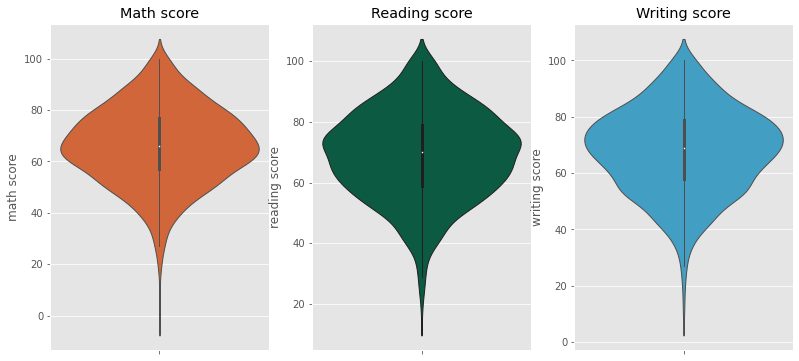
Most of the students score in between 60-80 in Math, whereas in Reading and Writing most of them score from 50-80.

2.2. Bivariate analysis 2.2.1. Categorical and categorical variable

gender
race/ethnicity
parental level of education
lunch
test preparation course

Chi-Square Statistic

from scipy import stats
from scipy.stats import chi2_contingency

The null hypothesis of the Chi-Square test is that no relationship exists on the categorical variables in the population.

Is the p-value less than .05? If so, we can conclude that the variables are not independent of each other and that there is a statistical relationship between the categorical variables.

The null hypothesis Ho: gender and  race/ethnicity are independent
The chi square value is 9.02738626908596
The p-value is 0.06041858784847785
gender and race/ethnicity are independent
-------
The null hypothesis Ho: gender and  parental level of education are independent
The chi square value is 3.384904766004173
The p-value is 0.6408699721807456
gender and parental level of education are independent
-------
The null hypothesis Ho: gender and  lunch are independent
The chi square value is 0.37173802316040705
The p-value is 0.5420584175146086
gender and lunch are independent
-------
The null hypothesis Ho: gender and  test preparation course are independent
The chi square value is 0.015529201882465888
The p-value is 0.9008273880804724
gender and test preparation course are independent
-------
The null hypothesis Ho: race/ethnicity and  parental level of education are independent
The chi square value is 29.45866151909779
The p-value is 0.07911304840592065
race/ethnicity and parental level of education are independent
-------
The null hypothesis Ho: race/ethnicity and  lunch are independent
The chi square value is 3.4423502326273185
The p-value is 0.48669808284196503
race/ethnicity and lunch are independent
-------
The null hypothesis Ho: race/ethnicity and  test preparation course are independent
The chi square value is 5.4875148857070695
The p-value is 0.24082911295018397
race/ethnicity and test preparation course are independent
-------
The null hypothesis Ho: parental level of education and  lunch are independent
The chi square value is 1.1112675079168055
The p-value is 0.9531014927218224
parental level of education and lunch are independent
-------
The null hypothesis Ho: parental level of education and  test preparation course are independent
The chi square value is 9.54407054307069
The p-value is 0.08923388625809343
parental level of education and test preparation course are independent
-------
The null hypothesis Ho: lunch and  test preparation course are independent
The chi square value is 0.22095439044844808
The p-value is 0.6383136809999865
lunch and test preparation course are independent
-------

We can see that all categorical variables are independent.

It appears that the association between these categorical variables are very weak.

Numerical and numerical variables

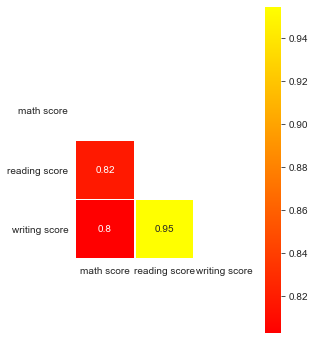
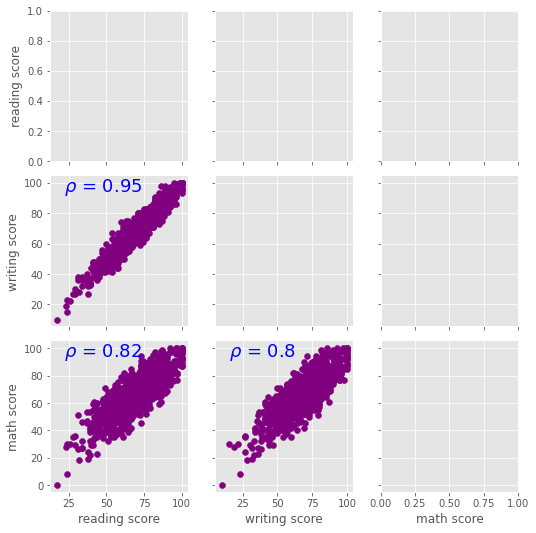
Correlation between scores

In statistics, the Pearson correlation coefficient (PCC, pronounced /ˈpɪərsən/), also referred to as Pearson's r, the Pearson product-moment correlation coefficient (PPMCC), or the bivariate correlation, is a measure of linear correlation between two sets of data.

import seaborn as sns
sns.pairplot(df, corner=True)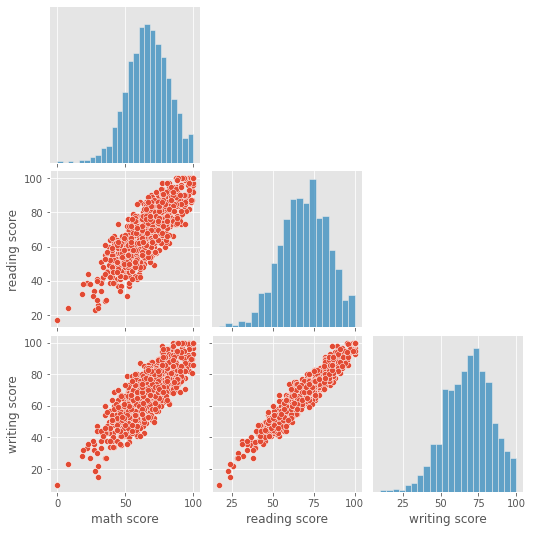

Questions to answer¶

Question 1: Proportion of students who passed the test

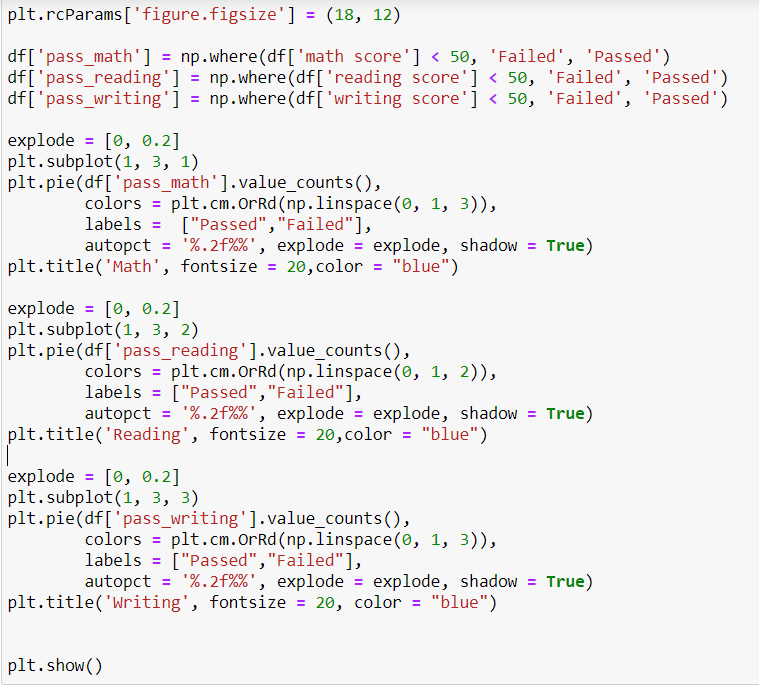
Math seems to be the most difficult subject when compared to Reading and Writing.

Question 2:

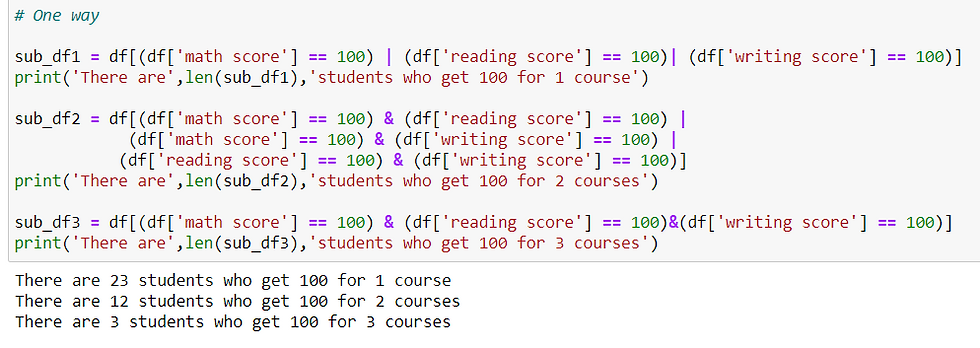
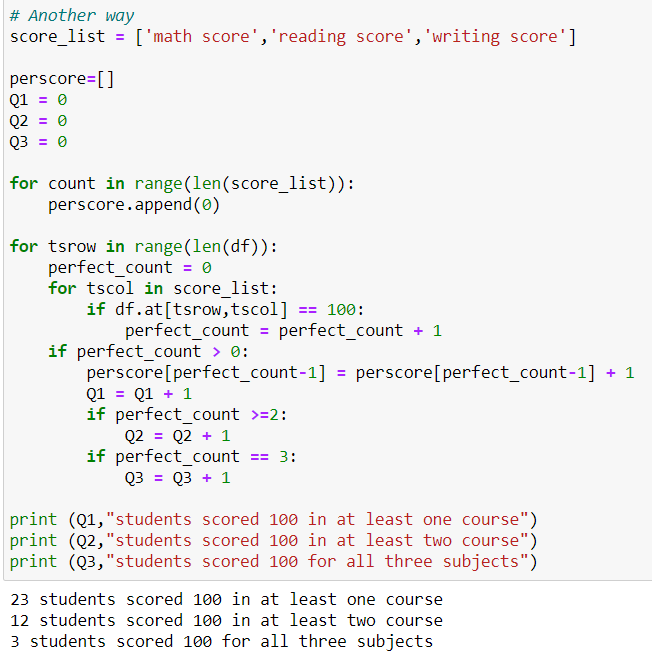
How many students scored 100 in at least one course?
How many students scored 100 in at least two courses?
How many students scored 100 for all three subjects?

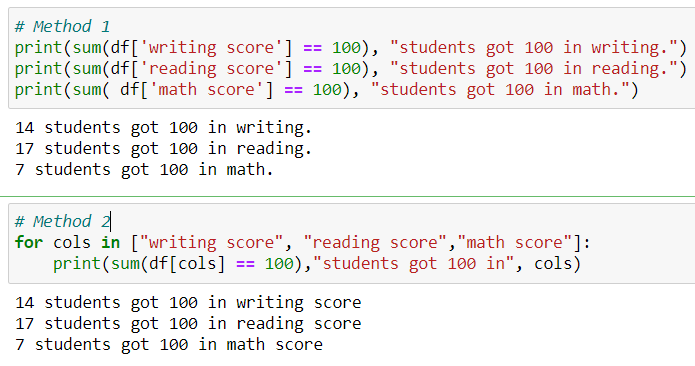
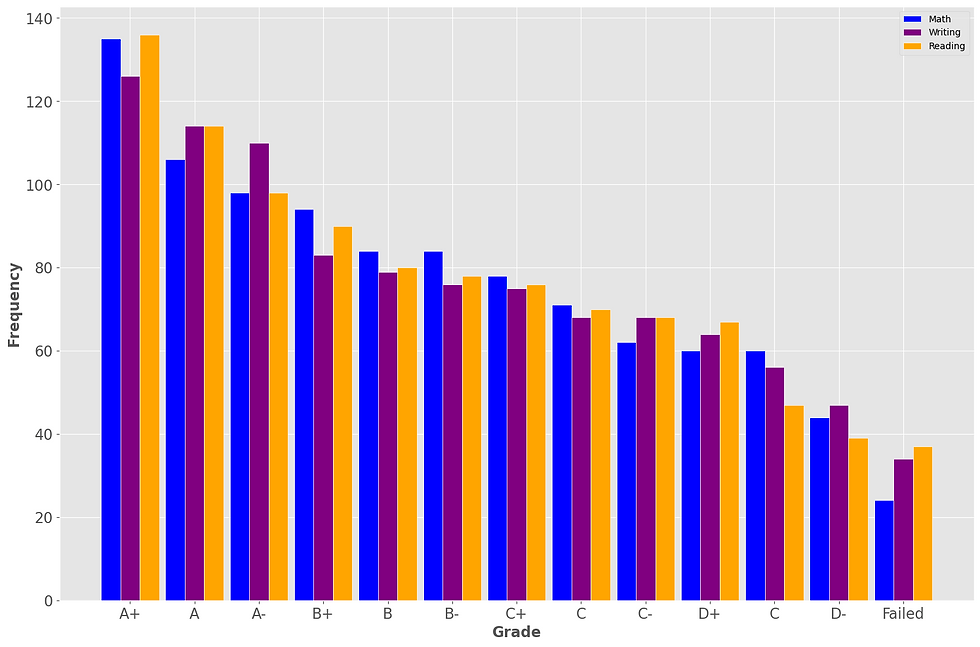
Question 3: How many students got 100 for each subject ?

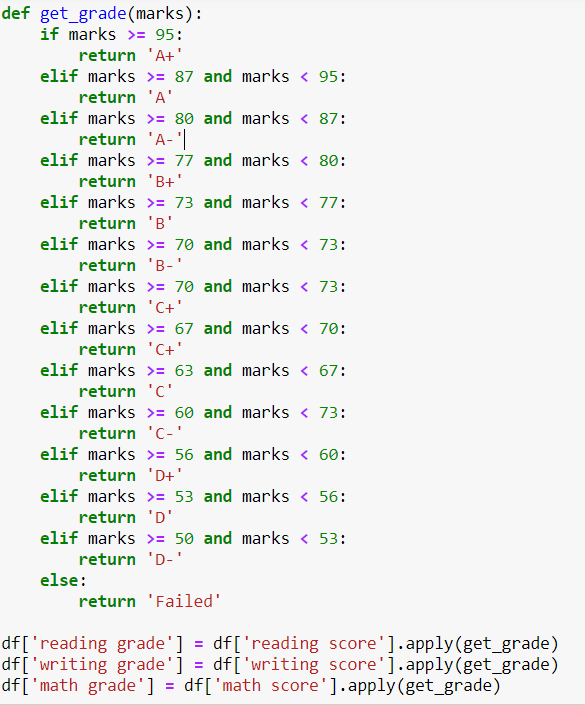
Adding columns for grade

Multivariate analysis (numerical and categorical)

import pylab
import scipy.stats as stats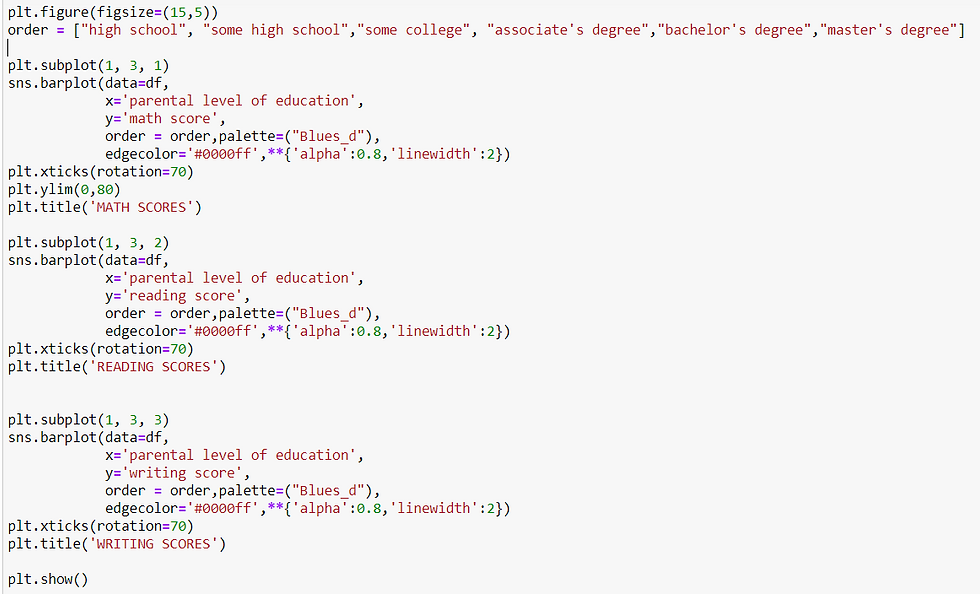

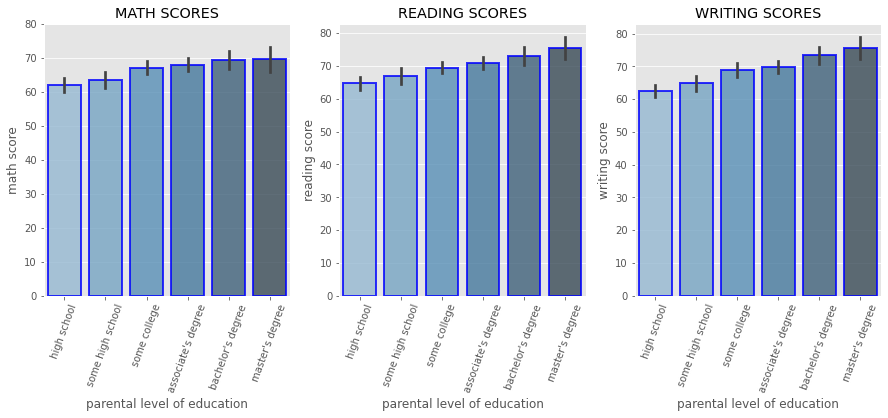
for i in ['math score','reading score','writing score']:
    plt.figure(figsize=(6,5))
    sns.boxplot(x = 'race/ethnicity', y = i, 
                data = df,
                order = ["group A","group B","group C","group D","group E"])
    plt.tight_layout()

columns_list = ['math score','reading score','writing score']

for i in columns:
    plt.figure(figsize=(6,6))
    sns.boxplot(data = df,
                x = 'gender', 
                y = i)
    plt.tight_layout()

Three variables

sns.pairplot(df , hue='race/ethnicity')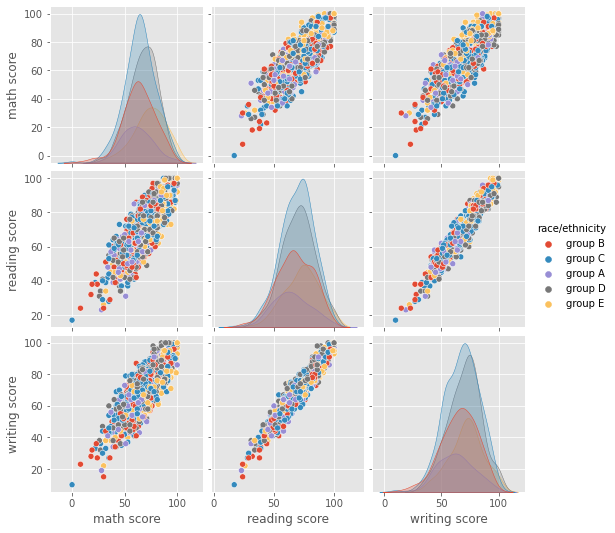

Other Datavis

plt.figure(figsize=(7,7))

plt.pie(df['race/ethnicity'].value_counts().values,
        explode = [0,0,0.1,0,0],
        labels = df['race/ethnicity'].value_counts().index,
        colors = ['#2085ec','#72b4eb','#0a417a','#8464a0','#cea9bc'],
        autopct = '%1.1f%%')

plt.title('Race/Ethnicity According Analysis', color='black', fontsize = 12)
plt.show()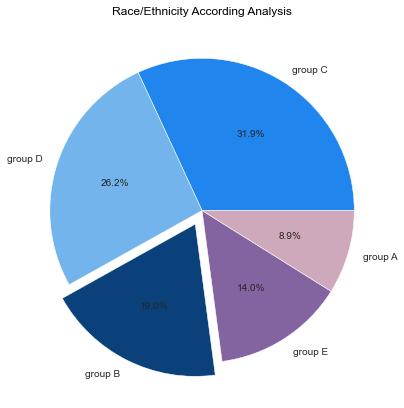

race = ['Group A', 'Group B ', 'Group C', 'Group D', 'Group E'] 

data = [89, 190, 319, 262, 140] 

colors = (  "#ffd11a", "#b463cf", 
          "#DC143C", "#6699ff", "#ff66b3" ) 
  
wp = { 'linewidth' : 1, 'edgecolor' : "#cccccc" } 
  
def func(pct, allvalues): 
    absolute = int(pct / 100.*np.sum(allvalues)) 
    return "{:.1f}%\n({:d} )".format(pct, absolute) 

fig, ax = plt.subplots(figsize =(15, 10)) 

wedges, texts, autotexts = ax.pie(data,  
                                  autopct = lambda pct: func(pct, data), 
                                  labels = race, 
                                  shadow = True, 
                                  colors = colors, 
                                  startangle = 90, 
                                  wedgeprops = wp, 
                                  textprops = dict(color ="#000000")) 
  
ax.legend(wedges, race, 
          title ="Race/Ethnicity", 
          loc ="center left", 
          bbox_to_anchor =(1.25, 0, 0, 1.25)) 
  
plt.setp(autotexts, size = 15, weight ="bold") 
ax.set_title("Race/Ethnicity Distribution", fontsize=15, fontweight='bold') 
  
plt.show()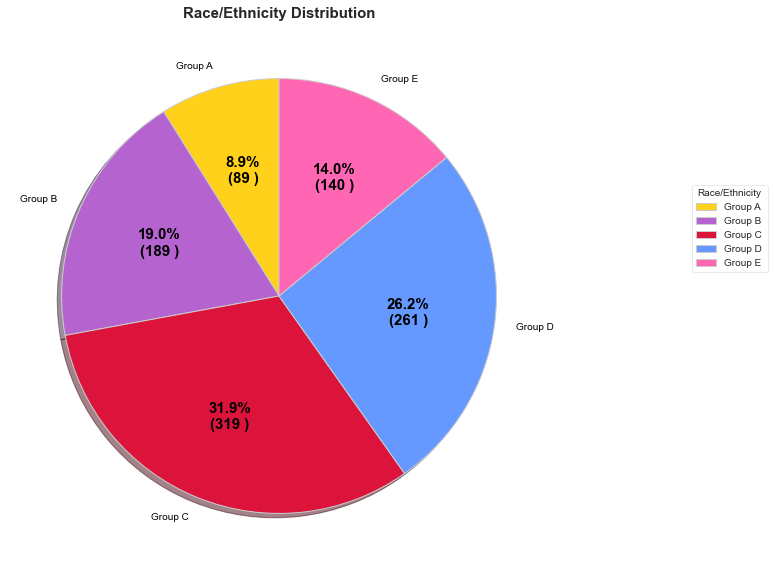

sns.catplot(x="test preparation course",
            y="reading score", 
            kind='violin', 
            hue='gender', 
            split='true', 
            data=df, height=6, aspect=2);
plt.grid()

sns.relplot(x='math score',y='reading score',hue='gender',data=df)

Research analyst
Data analyst
Data storyteller

Student Performance Analysis

1. First look at the data

To get a concise summary of the dataframe

For quickly testing if your object has the right type of data in it

Column Name Description

Examine missing values

2. Initial data exploration

Visualization of numerical variables

Calculating mean across groups

Numerical and numerical variables

Correlation between scores

Questions to answer¶

Question 1: Proportion of students who passed the test

Question 2:

Question 3: How many students got 100 for each subject ?

Adding columns for grade

Multivariate analysis (numerical and categorical)

Three variables

Other Datavis

Recent Posts

Comments

Research analyst Data analyst Data storyteller

1. First look at the data

To get a concise summary of the dataframe

For quickly testing if your object has the right type of data in it

Column Name Description

Examine missing values

2. Initial data exploration

Visualization of numerical variables

Calculating mean across groups

Numerical and numerical variables

Correlation between scores

Questions to answer¶

Question 1: Proportion of students who passed the test

Question 2:

Question 3: How many students got 100 for each subject ?

Adding columns for grade

Multivariate analysis (numerical and categorical)

Three variables

Other Datavis

Comments

Research analyst
Data analyst
Data storyteller